Introduction
In the using built-ins lesson, we learned some approximate quantifications of the number of libraries and modules we can use in Python. The take-away: there are lots of them, and if there is a well-tested, trusted library that solves all or part of our problem at hand, we should use it.
There is an avoidable issue with performance related to the use of libraries
like this. Suppose we need to calculate a square root of a value x. We would
access the library with import math, and then do the calculation via the
math.sqrt(x) function call. The Python interpreter has to look into the
math module, find the sqrt() function, and then execute the code. The
problem, performance-wise, is that process happens every time the function
is used, i.e., the Python interpreter does not remember that it has already
looked up the sqrt() function. This is costly if the function call look-up
happens inside of a loop.
Consider this code that creates a list of n pseudo-random values in the range [0, 1). We have not implemented the tips from the list comprehension lesson here.
1
2
3
4
5
6
# Sample 1 - naive creation of list of random values.
# n contains the number of values to create
values = []
for i in range(n):
values.append(random.random())
Using aliases to prevent repeated look-ups
To improve the performance of the code in Sample 1, we can use an alias,
which is where we have more than one name for the same object. In Sample 1,
random.random is the name of a function object that produces a pseudo-random
number in the range [0, 1). To prevent repeated look-ups of the function,
we can remember the name of the function in our own code via an alias,
as shown in Sample 2:
1
2
3
4
5
6
7
# Sample 2 - creation of list of random values with aliases
# n contains the number of values to create
values = []
rand = random.random
for i in range(n):
values.append(rand())
In Sample 2, we assign an alias, a.k.a. another name, for the random number
generating function with the rand = random.random statement.
Note how we do not include parentheses here! If we did this,
rand = random.random(), Python would execute the function, and our name
rand would be a random number between 0 and 1. Without the parentheses,
Python simply gives another name, of our own choosing, to the function.
The performance implication is that now, instead of having to look into
the random module each time to find the required function, the Python
interpreter can access the function via the local name rand.
Incorporating previous lessons
Before we examine the speedup caused by using aliases, let us see what happens when we also use list comprehension in our list creating code. First, Sample 3 shows code to create the list of random numbers, with list comprehension, but without using aliases:
1
2
3
# Sample 3 - creation of list with list comprehension but no aliases
# n contains the number of values to create
values = [random.random() for i in range(n)]
Sample 4, which uses both list comprehension and an alias for random.random,
should be the fastest version of this code so far.
1
2
3
4
# Sample 4 - creation of list with list comprehension and aliases
# n contains the number of values to create
rand = random.random
values = [rand() for i in range(n)]
The following graph shows the time taken by each of the four samples for a variety of list sizes, and the speedup comparing Sample 1 with Sample 4. We can see from the graph that using list comprehension and an alias for our function results in code that is almost twice as fast as the naive code in Sample 1.
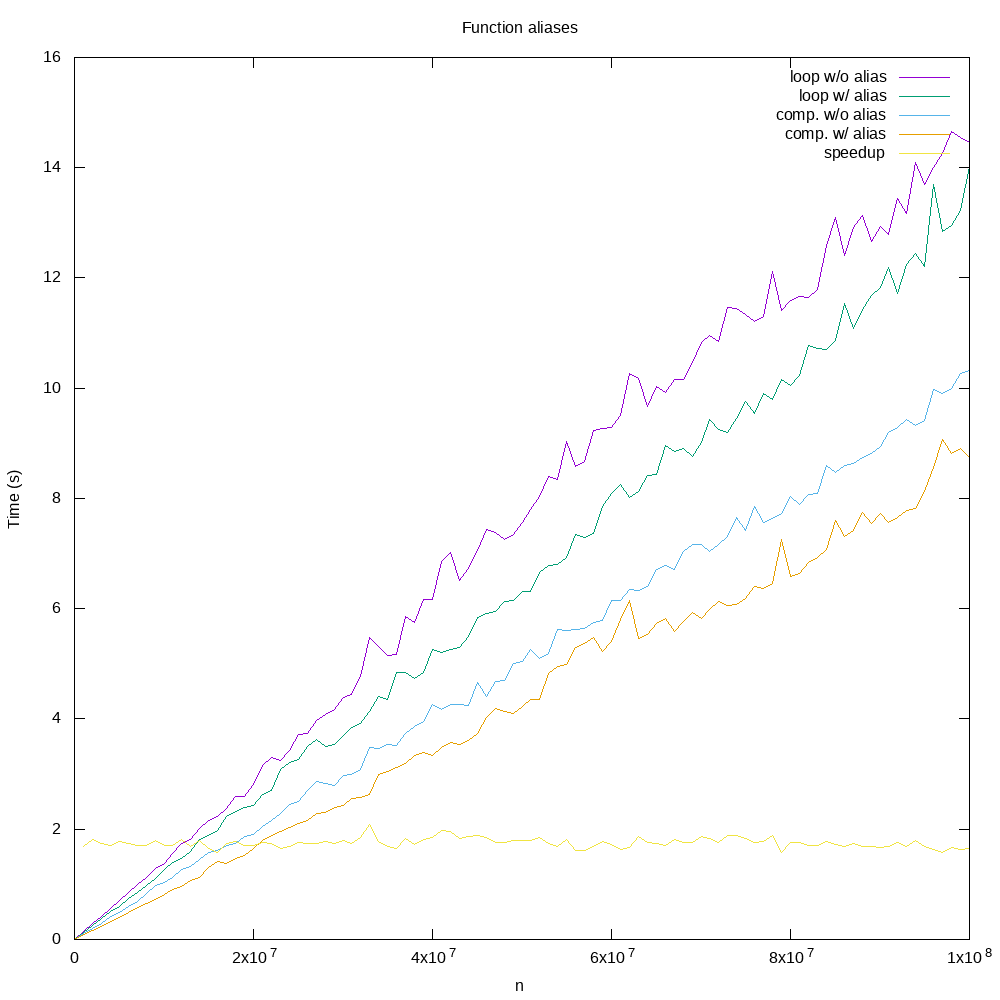
Tip: If you are using the dot (.) operator to access a function or some
other object in a module, and you are doing so inside a loop, consider using
an alias to improve your code’s performance.
Exercise
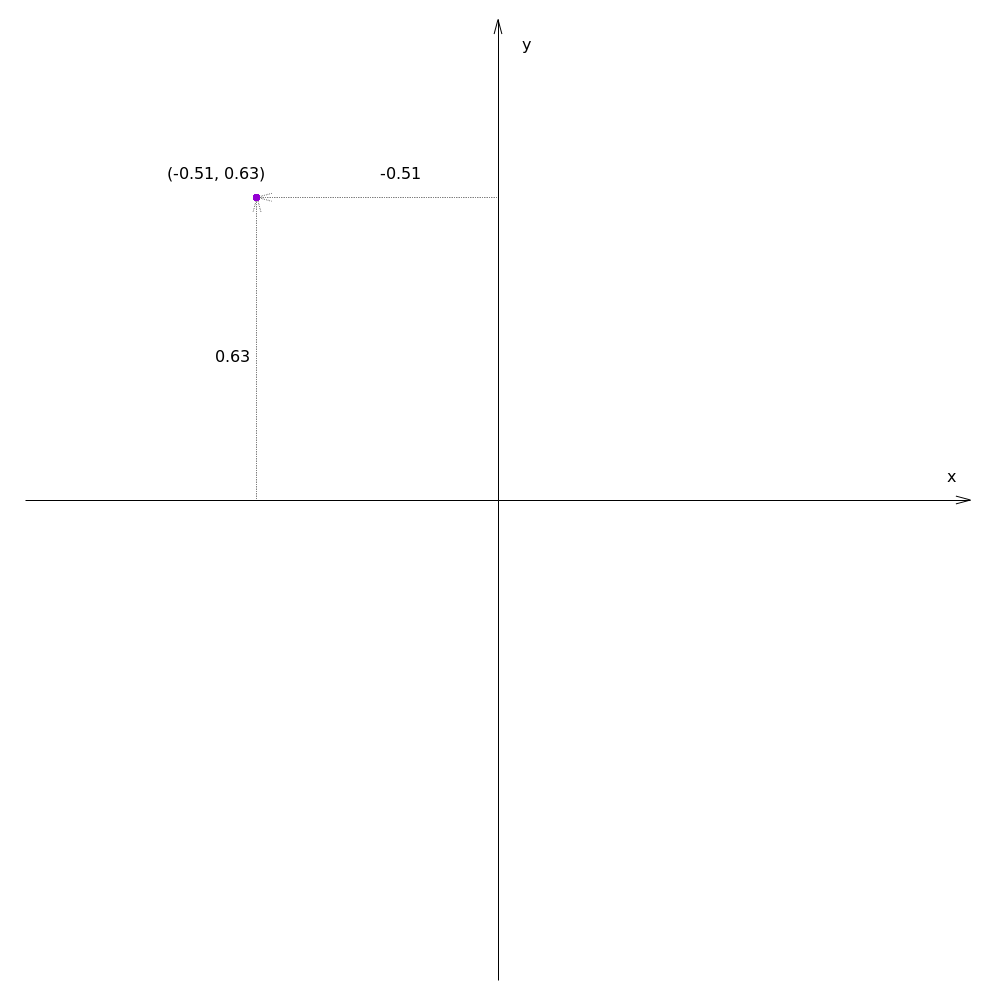
You are probably familiar with the Cartesian coordinate system, where the coordinates of a point on a plane are specified by the distance of the point from the x and y axes, respectively. For example, this image shows the Cartesian coordinates for a point with a negative x and positive y value.
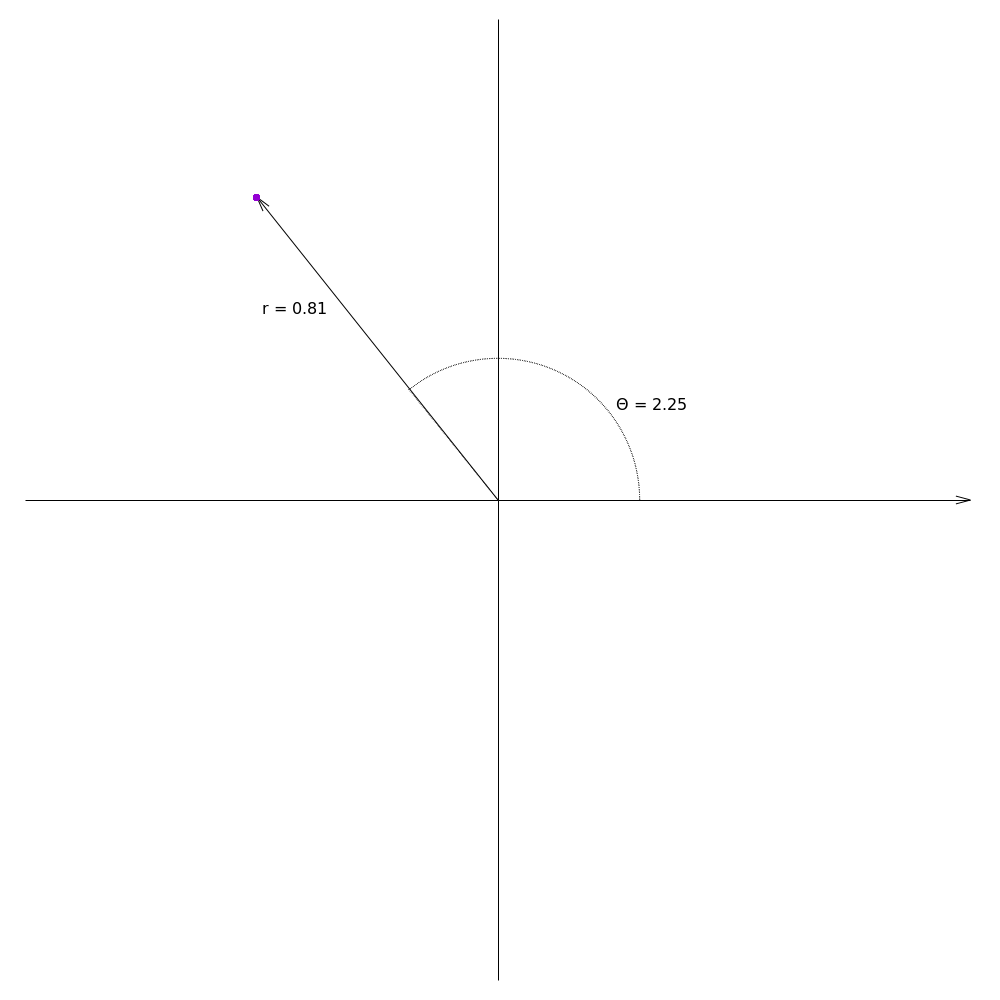
In some mathematical, physics, and computing applications, we often would rather work with polar coordinates, where the coordinate is specified by the angle from the rightward facing axis and the distance from the point to (0, 0). This figure shows the polar coordinate equivalent of the point in the previous image:
The sample code below creates a large list of randomly-generated Cartesian points
in the unit square, i.e., each point is in [1, 1]. Look up how to convert
Cartesian coordinates to polar, and then write code to produce a new list containing
(r, Θ) polar coordinates for each of the Cartesian points in the list
named cartesians. Use list comprehension and aliases to make the code work
faster.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
'''
Function alias exercise
Convert cartesian coordinates to polar.
'''
import math
import random
# create n cartesian coordinates in the unit square
n = 1_000_000
uni = random.uniform
cartesians = [(uni(-1, 1), uni(-1, 1)) for i in range(n)]
# write code here to create a new list called polars.
# the new list should contain the polar coordinate
# equivalents of each of the coors in cartesians.
Speedup
We refer to speedup as a way to compare our optimized code with its original, slower counterpart. Speedup is a measure of how well we have improved the runtime of our code. If T0 is the time taken by the original code, and T1 is the time taken by the improved code, then speedup is defined as
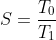
A speedup of 2 would mean that our optimized code is twice as fast as the original, while any value under 1 would mean that we actually made our code slower!
All performance figures on this page were obtained on a Windows 10 PC with an Intel® Core™ i5-9600K CPU @ 3.70GHz and 32GB of RAM, in Python 3.6.9 running in an Ubuntu Windows Subsystem for Linux environment.
Next lesson
The next lesson in the workshop is about aggregate functions