Introduction
Another way to speed up our Python code is to reduce the number of times a function is called. This is easy to do if we have a function that is to be applied to each member of a list. Our first instinct in that situation might be to use a loop or list comprehension to call the function on each element in the list.
Consider Sample 1, which converts a list of Cartesian-coordinate (x, y) tuples to polar (r, Θ) tuples. (If you have not yet gone through the function alias lesson, you should do so, and complete that lesson’s exercise before looking at the samples in this lesson.)
In Sample 1, lines 3 through 6 define the cartesianToPolar() function, which
takes a Cartesian tuple and returns an equivalent polar tuple. Note that the
optimization tips we have covered so far do not help us in this function – there
is no list to use comprehension
on, and using aliases won’t help,
since there is only one lookup of each math module function required.
Line 8 of the code creates a list of random Cartesian points, and line 10
uses list comprehension to apply the cartesianToPolar() function to each,
creating a new list called polars.
1
2
3
4
5
6
7
8
9
10
# Sample 1 - item-wise Cartesian to polar coordinates
# n contains number of coordinates
def cartesianToPolar(point):
theta = math.atan(point[1] / point[0])
r = math.sqrt(point[0] ** 2 + point[1] ** 2)
return (theta, r)
euclideans = [(random.random(), random.random()) for i in range(n)]
polars = [cartesianToPolar(p) for p in euclideans]
Apply functions to the list versus each item
The primary optimization tip here is to make the list the parameter of the
function, rather than an item in the list. That way, we call the function
one time, versus calling it n times. Sample 2 shows this tip in practice;
the cartesianToPolar() function now takes a list of tuples as its
parameter, instead of a single point. The function uses list comprehension
to built the list of polar coordinates to return, applying the same
conversion formula as Sample 1.
1
2
3
4
5
6
7
8
# Sample 2 - list-wise Cartesian to polar coordinates
# n contains number of coordinates
def cartesianToPolar(points):
return [(math.atan(point[1] / point[0]), math.sqrt(point[0] ** 2 + point[1] ** 2))
for point in points]
euclideans = [(random.random(), random.random()) for i in range(n)]
polars = cartesianToPolar(euclideans)
Incorporating previous lessons
You may have noticed a way that we can improve the performance of the list
comprehension in lines 4 and 5 of Sample 2: aliases. Each time a new polar
coordinate tuple is created for the return list, the Python interpreter
must look in to the math module to find the atan() and sqrt()
functions. We can improve our performance by creating local names for
these functions, thus looking each up only once, instead of n times.
This idea is applied in Sample 3 below.
1
2
3
4
5
6
7
8
9
10
# Sample 3 - list-wise Cartesian to polar coords, w/ aliases
# n contains number of coordinates
def cartesianToPolar(points):
at = math.atan
sqt = math.sqrt
return [(at(point[1] / point[0]), sqt(point[0] ** 2 + point[1] ** 2))
for point in points]
euclideans = [(random.random(), random.random()) for i in range(n)]
polars = cartesianToPolar(euclideans)
In Sample 3, lines 4 and 5 declare local names for math.atan and math.sqrt:
at and sqt, respectively. Then the list comprehension in lines 6 and 7
uses these local names to form the return list of polar coordinate tuples.
We expect Sample 3 to be faster than Sample 2, which in turn is expect to
be faster than Sample 1.
Tip: If you need to apply one of your own functions to all of the values in a list, consider re-designing your function so that you can pass the whole list to the function instead of passing a single list element.
We can go even faster, though.
Ignoring a previous lesson
In the using built-ins lesson, we encouraged programmers to use the built-in capabilities of Python, and / or trusted, well-tested modules and libraries, to improve the performance of their code. Sometimes, however, we can improve the speed of our code by breaking that “rule.”
In the conversion formula in line 6 of Sample 3, the code is computing the r value for the polar coordinate by calculating this formula:

In Sample 3, we are taking advantage of the built-in Python exponentiation
operator, **. The problem is that ** is a powerful, general-purpose
operator that is overkill for the problem at hand. Since computing
x2 is the same as x × x, we can actually improve
our performance by using multiplication instead of the exponentiation
operator. This is shown in Sample 4.
1
2
3
4
5
6
7
8
9
10
# Sample 4 - list-wise Cartesian to polar coords, w/ alias, w/o **
# n contains the number of coordinates
def cartesianToPolar(points):
at = math.atan
sqt = math.sqrt
return [(at(point[1] / point[0]), sqt(point[0] * point[0] + point[1] * point[1]))
for point in points]
euclideans = [(random.random(), random.random()) for i in range(n)]
polars = cartesianToPolar(euclideans)
Line 6 of Sample 4 has replaced exponentiation with multiplication. Now, let us take a look at the performance of these four versions of the same code. The following graph shows the time taken by each of the four samples for a variety of list sizes, and the speedup comparing Sample 1 with Sample 4. We can see from the graph that applying the function in aggregate, using aliases, and using multiplication instead of exponentiation is approximately 1.5 times as fast as the naive code in Sample 1.

Tip: Calculating the square of a value via multiplication is faster than using the exponentiation operator to accomplish the same task.
Exercise
In machine learning, one task we frequently have to perform is to clean data,
by removing data points that, for one reason or another, cannot be input to
our machine learning model. This exercise is a simple taste of data cleaning.
The code shown below creates a list of numbers which are supposed to be in
the range [0, 1). However, a certain percentage of the values are invalid.
The validateElement() function determines if a given value is valid or not.
Then, in the main program, line 60 creates a new list that contains only valid
data.
Your task in this exercise is to replace validateElement() with a function
that works on the entire list rather than elements of the list, and then to modify
the main program to use your new function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
'''
Aggregate function exercise.
'''
import random
def buildData(n, defectRate):
'''
Build a list of sample data in the range [0, 1).
A certain percentage of the elements will be outside
the range; these represent invalid data points.
parameters
----------
n - number of list elements
defectRate - percent of elements that are invalid
returns
-------
List of sample data with some invalid values.
'''
values = []
rand = random.random
for i in range(n):
if rand() <= defectRate:
if rand() <= 0.5:
values.append(-rand())
else:
values.append(1.0 + rand())
else:
values.append(rand())
return values
# TODO: replace this with a function that operates on
# the aggregate instead of individual elements
def validateElement(element):
'''
Determine if a single data point is valid.
parameter
---------
element - number supposed to be in [0, 1)
returns
-------
True if element is valid, False if it is not
in the specified range
'''
return element >= 0.0 and element < 1.0
# main program
n = 10_000_000
defectRate = 0.01
# build sample data
originals = buildData(n, defectRate)
# TODO: replace this with a call to your new function
# filter data
filteredData = [x for x in originals if validateElement(x)]
Speedup
We refer to speedup as a way to compare our optimized code with its original, slower counterpart. Speedup is a measure of how well we have improved the runtime of our code. If T0 is the time taken by the original code, and T1 is the time taken by the improved code, then speedup is defined as
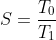
A speedup of 2 would mean that our optimized code is twice as fast as the original, while any value under 1 would mean that we actually made our code slower!
All performance figures on this page were obtained on a Windows 10 PC with an Intel® Core™ i5-9600K CPU @ 3.70GHz and 32GB of RAM, in Python 3.6.9 running in an Ubuntu Windows Subsystem for Linux environment.